DISEÑO, CONSTRUCCIÓN Y CONTROL
DE UN ROBOT PARALELO DE TRES GRADOS DE LIBERTAD
Continuación...
ROBOT PARALELO DELTA
El caso de estudio de este trabajo es un robot paralelo
tipo Delta. La estructura de este robot está definida
en (Clavel, 1991), en la figura 2 se muestran los principales
elementos de este robot.
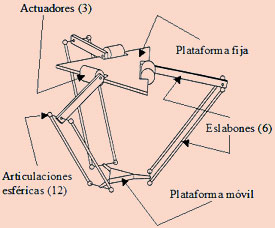 |
| Figura 2. Desplazamientos del
robot paralelo Delta |
Se trata de un robot
de triple grado de libertad, que permite solamente movimientos
de traslación para la plataforma móvil.
Los tres actuadores son servomotores de corriente directa
y están firmemente montados sobre una plataforma
fija, su eje está acoplado a un eslabón
superior. Cada una de las tres cadenas cinemáticas
está formada por un motor (articulación
rotacional activa), un eslabón superior y un eslabón
inferior unidos mediante un par de articulaciones esféricas
(pasivas). El eslabón inferior se une a la plataforma
móvil mediante otro par de articulaciones esféricas
(pasivas). En el eje de cada motor se encuentra acoplado
un eslabón. El elemento terminal del robot (herramienta
o pinza) se ubica sobre la plataforma móvil. El
movimiento sincronizado de las articulaciones activas
permite posicionar en el espacio a la plataforma móvil,
aunque la orientación permanece constante.
La figura 3 muestra dos
posibles desplazamientos del robot, el primero corresponde
al robot completamente contraído, el segundo al
robot completamente extendido.
En tareas de seguimiento de trayectorias,
el estudio de la cinemática debe centrarse en el
análisis de la cinemática inversa, es decir
encontrar el ángulo de rotación de cada
motor a partir del conocimiento de la posición
deseada para el elemento terminal del robot (Márquez,
2002). La cinemática inversa para el robot Delta
se realiza a partir del análisis de una cadena
cinemática, como se muestra en la figura 4. En
esa figura, los eslabones superior e inferior tienen longitudes
LA y LB respectivamente y están unidos en el punto
Ci. La longitud R es la distancia entre el centro del
eje de giro del servomotor y el centro de la plataforma
fija Cf. El ángulo qi es un valor constante e indica
la orientación del eje de cada servomotor. El punto
Ai es el centro del eje de giro del servomotor. El ángulo
ai es la variable articular y representa el ángulo
de giro del servomotor. El punto Pi es la unión
del eslabón inferior y la plataforma móvil.
Realizando las consideraciones geométricas adecuadas,
se puede obtener el ángulo ai que deben girar los
motores para que el robot alcance una posición
en el espacio definida por las coordenadas xp, yp, zp
de la plataforma móvil:
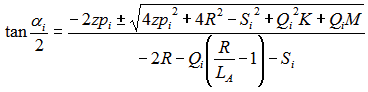
donde:
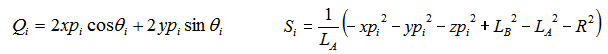
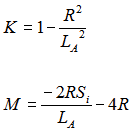
Siguiente...

